Unraveling the Mysteries of Place Value and Rounding

June 18, 2024 – KasiMaths

In today’s edition of KasiMaths Corner, we delve into the fascinating world of numbers, exploring two fundamental concepts: place value and rounding. Mastery of these concepts not only bolsters our mathematical skills but also equips us with essential problem-solving abilities for everyday life. Let’s dive right in!

Understanding Place Value

Place value is a foundational principle in mathematics. It helps us comprehend the relative worth of digits within a number, much like a hierarchy where each place holds its unique importance.

Identifying Place Value

To understand place value, we start from the rightmost digit, known as the units place. As we move left, each digit holds a place value ten times greater than the one to its right. For example, consider the number 3,215,467:

• 7 is in the units place
• 6 is in the tens place
• 5 is in the hundreds place
• 4 is in the thousands place
• 1 is in the ten thousands place
• 2 is in the hundred thousands place
• 3 is in the millions place

Understanding place value is crucial for reading and writing large numbers accurately and for performing arithmetic operations effectively.

Decimal Numbers

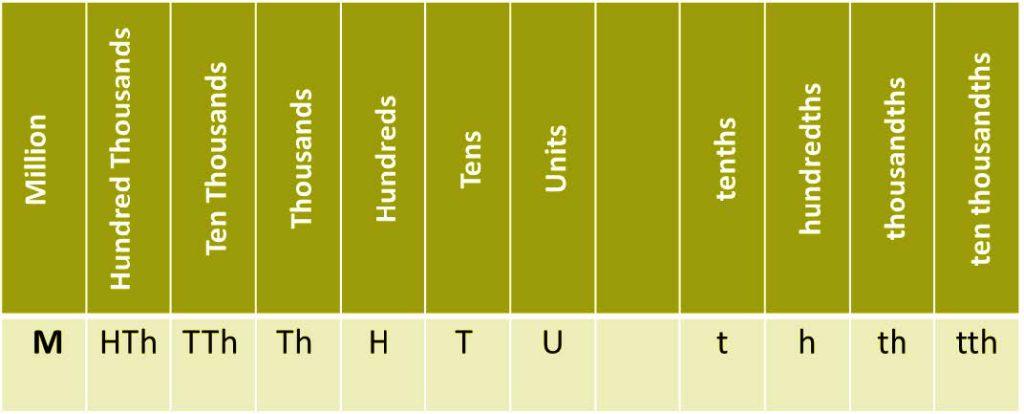
For decimal numbers, the logic of place value extends to the right of the decimal point, where each place value is a power of 10 but in the negative direction. For instance, in the number 3.215:

• 3 is in the units place
• 2 is in the tenths place
• 1 is in the hundredths place
• 5 is in the thousandths place

Decimals are vital for representing values smaller than one and are commonly used in measurements, currency, and scientific data.

The Art of Rounding Numbers

Rounding numbers is an essential skill for making estimates and approximations. Here’s how it works:

Rounding Integers

To round an integer to the nearest ten, hundred, or thousand, focus on the digit in the place value you’re rounding to. If the digit to its right is 5 or greater, round up; otherwise, round down. For example, rounding 3,215,467 to the nearest thousand gives us 3,215,000.

Rounding Decimals

Rounding decimal numbers involves the same principles. For instance, rounding 3.215 to the nearest hundredth results in 3.22.

Rounding Money

When rounding money, adhere to standard currency rounding rules. For example, rounding $3.567 to the nearest cent gives us $3.57.

Rounding to a Set Number of Decimal Places

Sometimes, specific precision is required. For example, rounding 3.215 to two decimal places results in 3.22.

Practical Applications and Exercises

Let’s apply these concepts with practical examples:

1. Identify the place value of the underlined digit in the number 5, _3_14,792.
2. Round the number 7,349 to the nearest hundred.
3. Round the decimal 4.6789 to the nearest tenth.
4. Round $45.678 to the nearest cent.
5. Round 9.4321 to two decimal places.

Answers

1. The place value of the underlined digit (3) is the hundred thousands place.
2. Rounding 7,349 to the nearest hundred gives us 7,300.
3. Rounding 4.6789 to the nearest tenth gives us 4.7.
4. Rounding $45.678 to the nearest cent gives us $45.68.
5. Rounding 9.4321 to two decimal places gives us 9.43.

Conclusion

Congratulations, readers! You’ve now unlocked the mysteries of place value and rounding. These foundational skills will serve as your compass as you navigate the vast landscape of mathematics. Remember, practice makes perfect, so apply these concepts in your daily encounters with numbers. Until next time, keep exploring and keep learning!

Stay tuned for more insights and tips in our next edition of KasiMaths Corner!